Accepting Conventional Wisdom

There are some people who claim to believe that they don't accept the conventional wisdom that we live on an essentially ball-shaped planet but rather on a large disc, so-called 'flat earthers'.

I rather suspect that they only 'claim to believe' in order to get 'round earthers' to justify their belief in the Earth being a globe and there are plenty of folks on YouTube and Facebook who try to do that, often with an exasperated tone.

In recent years I have come cross many cartoons pushing the idea of 'who do you believe, someone who has studied science or someone who saw something on the Internet?' Clearly these are intended to mock the 'ignorant' minority as opposed to those who 'follow the science'.

Passing on knowledge

The great benefit of language is that the human animal is able to pass on information to others; writing allows that information to be preserved beyond the lifetime of an individual; printing and its digital equivalents allows that information to be disseminated way beyond the immediate society of that individual.

This can be a great time-saver, which of two paths leads to the river? That information can be shared, it becomes part of a body of knowledge, no-one else has to take the time to discover the route to the river themselves. But what if that 'knowledge' is false, just assumed to be true and never challenged because that is what 'everyone' believes?

The typical scientist would have been taught science at school by a teacher that was also taught science at school, perhaps even using the same text books or at least text books that effectively are copies of earlier volumes. They were unlikely to have repeated every experiment described and even if they did their result will have been aligned with the conventional view, any anomaly just being 'experimental error'.

Teaching wrong science

Two events stand out in my own experience, one at university and one at grammar school. A demonstrator at university, wanting to hurry us out of the laboratory said, "You only need two results for a straight line!". That is true but one needs at least three results to have any degree of assurance that it is a straight line. At school we had all watched an experiment performed by a teacher in which he had set alight a candle inside a bell jar placed in a water bath. We were told that we had seen the water level rise as the burning candle had consumed the oxygen in the enclosed air. Bravely I put up my hand, ''But Sir, the water level went down first!". To his credit my teacher said, ''Why?" and it came to me straight away, ''Because the candle heated up the air which expanded and pushed the water down?".

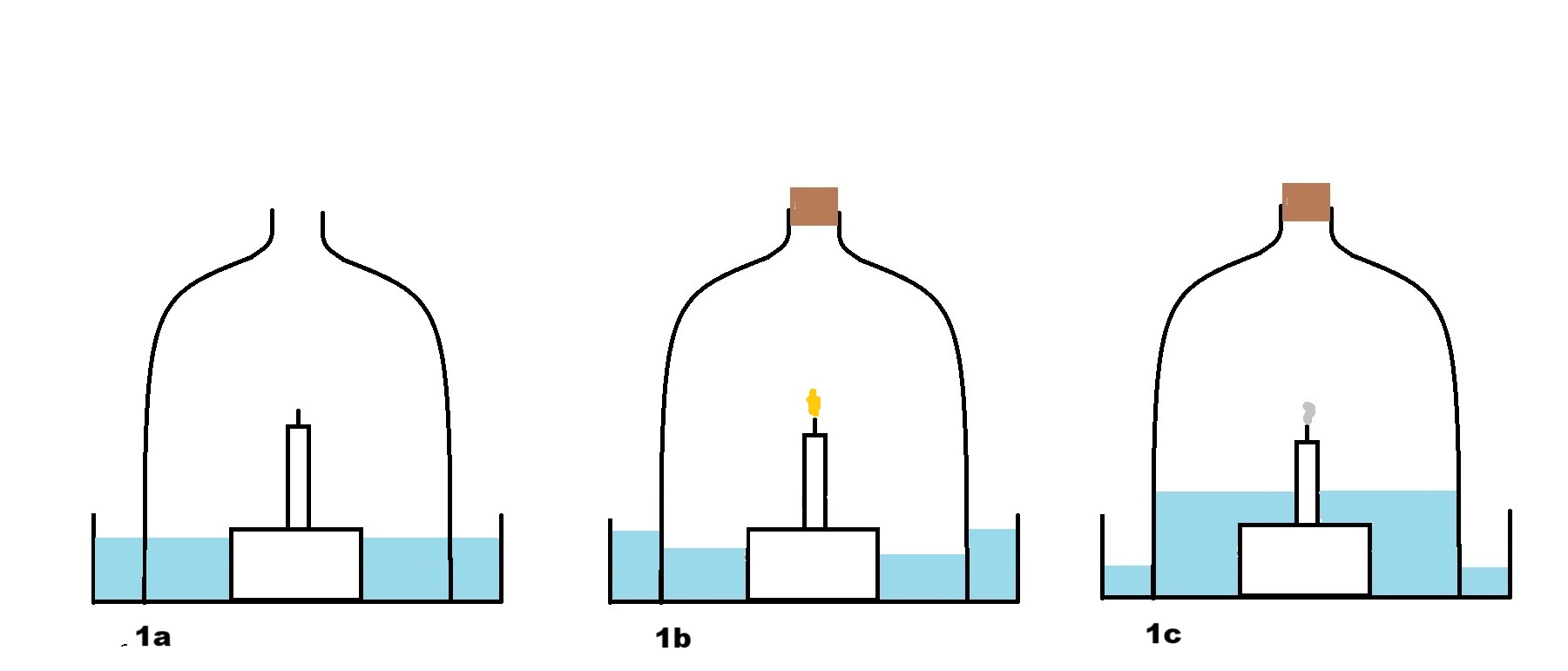
Without my intervention the whole class would have 'observed' what they were told without question. Potential teachers, scientists and text book writers would continue 'the science', a science that was incomplete.

Average students don't question; some become average teachers

I have a theory that a middle group of people have the ability to take in a given set of information without question and with a sufficient degree of understanding that they can pass examinations. For some this is way beyond their ability, they can never pass exams. Others are far beyond this, what they have been told is 'obvious' and possibly better understood by them than the teacher armed only with 'text book' knowledge. Tucked in there are some desperate to 'understand' before they can learn.

At school I struggled with 'pure' mathematics, in particular with 'standard results'. I would frustrate my teacher when I began every answer to a set question by using 'first principles'. I was told that there were three possible methods to solve the problem and that I was required to quickly select the best method and use it to get the solution, I didn't have time to start from my knowledge of 'first principles'. As I said before, most of the class somehow knew the 'standard results', plugged them in and achieved a solution. But did they know why?

Using learned knowledge

Many years later, at work, there were a few occasions when I realised that there was use for some of those things that I had been told in my Pure Mathematics class. Of course I had long forgotten, if indeed I ever knew, how to employ them so I had to dig out the text books. Having got a satisfactory answer I would tell a colleague what I had done and almost invariably they would say, "Ah yes, so-and-so's rule" and follow that by quoting the 'standard result' off pat.

Here we had people who membered the rule from perhaps twenty years earlier but never saw a need to employ it and myself who probably never knew the rule, let alone remembered it, but immediately saw where it could be applied! As I used to say to my teacher that me resorting to 'first principles' at least showed that I understood the 'why'. Were the others just performing by rote? How many of them went on to teach by rote?

Why the 'Flat Earthers' are right

The 'Flat Earthers' are right. They challenge the certainty of the 'Round Earthers', forcing them to seek counter arguments and experiments for themselves rather than just repeat the conventional wisdom, 'the science'.

The 'Round Earhers' that rise to the challenge are also right! We should question our understanding from time-to-time. Obviously we have to take most of what we have been taught on trust but true understanding probably starts from doubt and then explaining the 'why' to ourselves, or better yet, others.

Postscript

I think that sometimes the older text books are better than more recent ones, possibly as a result of teaching and learning by rote, scientific 'Chinese whispers', the truth gradually becoming degraded.

When I started studying Electrical and Electronic Engineering at university I had a sudden knowledge crisis, I didn't understand 'Ohms Law', the simplest of circuits, a battery and a resistor, the basis of the subject!

V = iR

A positive voltage (V) is produced by a positive current (i) flowing through a positive resistance (R), simple, but wrong!

Take a basic circuit, a battery connected to a resistor. The terminal voltage of the battery, conventionally represented as an e.m.f. E (electromotive force) drives a current, i around the circuit, through the resistance R which generates an opposing voltage V. This satisfies Kirchhoff's Second Law that requires the sum of all voltages around a circuit to be zero.

This has a parallel in Newton's Third Law of Motion, ''for every action there is an equal and opposite reaction".

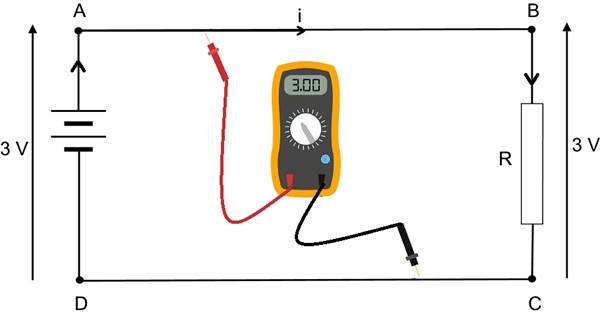
The 'sliding contact' voltmeter should make this clear. The red lead of the voltmeter is connected to the battery positive terminal and the black lead to the battery negative terminal. The positive reading can be represented by the vertical arrow alongside the battery. It should now be noted that the conventional current flow out of the battery can be represented by an in-line arrow in the same direction as the voltage arrow – the voltage is driving the current.

Now slide the voltmeter leads along the horizontal wires towards the resistor. The reading should be unchanged as the circuit wires A-B and C-D have no resistance. Electrically the resistor terminations are identical to the equivalent terminals of the battery. However the conventional current flow arrow is now pointing downwards, i.e. in opposition to the voltage.

Consider the three basic elements of an electrical circuit, resistance, inductance and capacitance. A positive flow of current through a resistor produces an opposing voltage, a positive rate of change of current through an inductor produces an opposing voltage and a positive integral of current with time (charge) into a capacitor produces an opposing voltage – nicely consistent!

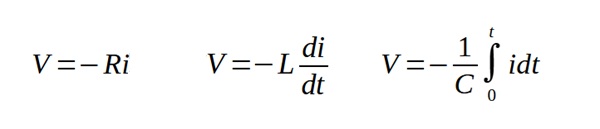
This text book starts in a promising way:

[Note: It should include electromagnetic or electrostatic energy.]

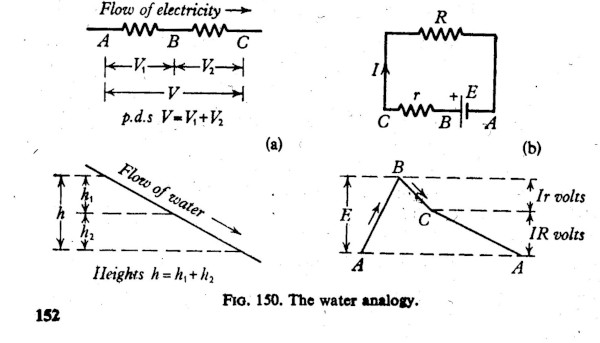
It tries to demonstrate this by a 'water analogy' – head of water being equivalent to voltage. The voltage gradient diagram correctly shows the resistive voltage drops opposing the driving voltage of the battery, however diagram (a) is ambiguous as the voltage 'arrows' are double-ended, giving no sense of polarity, hardly helping to make thing clear.

Like most text books when it comes to describing the action of coils it inserts a minus sign in the various equations, the so-called 'back e.mf.' ¹that most students will have heard of (and falsely believe to only exist in inductive circuits).

Then appears this most appalling note:

I would say that it is pretty important to know the direction of current flow and the polarity of voltages in all circuits!